Prawdopodobieństwo zdarzeń rzadkich
Wpis przeniesiony ze zlikwidowanej witryny
Prawdopodobieństwo zdarzeń rzadkich obliczamy używając wzoru Poissona.
Wzór Poissona
Obliczamy prawdopodobieństwo liczby k sukcesów w n-elementowej próbie. Korzystamy z wzoru Poissona:
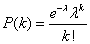
gdzie
n – jest liczebnością próby
k – jest zakładaną liczbą sukcesów
p – jest prawdopodobieństwem zdarzenia sprzyjającego
λ = n × p
e – jest liczbą Eulera = 2.718
! – oznacza silnię. Więcej o silni we wpisie: Java: jak implementować Callable?
Wzór Poissona jest stosowany gdy:
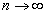
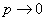
- Iloczyn λ = np jest wielkością stałą
- λ > 0
Przy stosowaniu wzoru n powinno być większe od 99, a λ < 21
Przykład 1
Zakładamy, że każda osoba cywilna spotkana z bronią na ulicy jest turystą. Prawdopodobieństwo p napotkania turysty wynosi 0.0001.
Policja rewiduje 1000 losowo wybranych osób. Jakie jest prawdopodobieństwo, że wśród tych osób będzie 2 turystów?
n = 1000
p = 0.0001
λ = n × p = 1000 x 0.0001 = 0.1
![]()
Przykład 2
Jakie jest prawdopodobieństwo, że w warunkach Przykładu 1 w badanej próbie znajdzie się co najwyżej (nie więcej niż) dwóch turystów.
Badane prawdopodobieństwo jest sumą trzech prawdopodobieństw:
- P(0) = nie zostanie złapany żaden turysta
- P(1) – zostanie złapany 1 turysta
- P(2) – zostanie złapanych 2 turystów
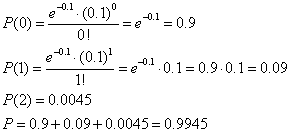
Copyright Jacek Piechota, Opublikowano 13 kwietnia 2016
A co z koronawirusem?
Moje przyjaciółki Aria i Suita z Terierogrodu pokazły jak ręcznie wyliczyć prawdopodobieństwo zarażenia się koronawirusem w Polsce we wpisie Prawdopodobieństwo zarażenia koronawirusem. A moja przyjaciółka Aria, programistka Java, umieściła tutaj blogu wpis Prawdopodobieństwo zarażenia (Java), w którym podaje metody ułatwiające obliczenia.

