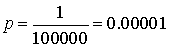Aria: Suitka, jesteś świetną matematyczką, najlepszą wśród psów i lepszą od wielu ludzi. Powiedz mi jakie jest prawdopodobieństwo zarażenia koronawirusem w Polsce?
Suita: Świetne pytanie. Aż zatarłam łapki. Przyjmijmy, że Polska ma 35 000 000 osób, jest 350 zarażonych, czyli 1 osoba na 100 000. Załóżmy, że mamy miasto mające 100 000 mieszkańców. Czyli możemy spodziewać się średnio 1 zarażonego.
Aria: Brzmi ciekawie.

Suita: Jak myślisz jakie jest prawdopodobieństwo zarażenia?
Aria: Jeżeli ktoś wyjdzie z domu 100 000 razy i za każdym razem spotka 1 osobę to spotka jedną zarażoną osobę.
Suita: Świetnie. Ale to trochę naiwne. Nie widzisz problemów?

Aria: Widzę. Ludzie podejmują decyzje więc układ nie jest całkiem losowy. Ponadto ludzie nie są rozmieszczeni losowo i nie wychodzą wszyscy o tej samej porze na miasto.
Suita: Bardzo mądrze. Zarażony może przecież mieszkać na tej samej klatce i zarazisz się za pierwszym wyjściem. Jest jeszcze jeden problem.
Aria: Jaki?
Suita: Jeśli w Polsce jest 350 zarażonych to w tym mieście może nie być żadnego zarażonego albo …
Aria: … albo mogą mieszkać wszyscy zarażeni lub dowolna część z nich. No to jak liczymy?
Suita: Możemy spróbować statystyki.
Aria: Czym różni się statystyka od rachunku prawdopodobieństwa?
Suita: Statystyka zajmuje się szacowaniem prawdopodobieństw. Im więcej próbek mieszkańców pobierzemy i im bardziej liczne będą próby, tym dokładniej oszacujemy liczbę chorych w mieście.
Aria: No to jaką metodę zastosujemy?
Suita: Na razie żadną. Mamy jeszcze jeden problem.

Aria: Jaki?
Suita: Jedna, a nawet 350 osób na 100 000 to bardzo mała proporcja. Prawdopodobieństwo jest bardzo małe. Możemy pobrać dużo licznych prób i nie znaleźć w niej żadnego chorego.
Aria: No to jak? Da się w końcu policzyć czy nie?
Suita: Coś ty taka niecierpliwa. Jasne, że się da. Pewien genialny matematyk z XIX wieku, Poisson (czytaj: płazo) , opisał rozkład, nazwany rozkładem Poissona, który służy własnie do szacowania w sytuacjach, gdy mamy do czynienia z dużymi liczbami, a małymi prawdopodobieństwami. Ten wzór ma bardzo dużo użytecznych zastosowań do całej gamy różnych wyliczeń.
Aria: No to liczmy!
Suita: Skorzystamy z wzoru Poissona.
Nasze parametry to:
n = 100 (zakładamy, że na spacerze spotkamy 100 osób)
![]() (proporcja osób zarażonych (liczba zarażonych/ liczbę mieszkańców)
(proporcja osób zarażonych (liczba zarażonych/ liczbę mieszkańców)
![]()
e = 2.718 (podstawa logarytmów naturalnych)
k = 1 (prawdopodobieństwo spotkania k osób zarażonych)
Podstawiamy wszystko do wzoru Poissona:
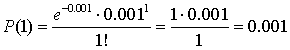
Aria: A jak policzyć prawdopodobieństwo dla 2, 3 itd.
Suita: Jesteś programistką, czy nie? Napisz algorytm w języku Java.
Aria: Już napisałam i umieściłam na pewnej witrynie. Tam też obliczyłam dokładnie powyższy wynik.
Aria: Prawdopodobieństwo jest bardzo małe. Ale jak zinterpretować wynik?
Suita: Obawiam się, że to sprawa czysto subiektywna. Inaczej wynik oceni młody, zdrowy człowiek, która ma szansę na wyleczenie, a inaczej stary, schorowany człowiek, dla którego zarażenie może skończyć się śmiercią.

Aria: Pozostawmy więc interpretację uznaniu naszych czytelników.
Suita: Ponadto wzór obowiązuje dla losowego rozkładu ludzi na ulicy. Jeśli pójdziesz do apteki lub na izbę przyjęć – dane do obliczenia zmienią się i oczywiście zmieni się wynik.
Aria: „Czucie i wiara silniej mówi do mnie niż mędrca szkiełko i oko” …
Suita: Jasne. Dopóki nie złapiesz koronawirusa …

ARIA: Podobno zapach fiołków odstrasza koronawirusa… Pani przynosi do swojej sypialni codziennie świeży bukiecik.