Java: Jak implementować Callable?
Wpis przeniesiony ze zlikwidowanej witryny
Problem
Silnia
silnia = factorial (ang.).
n! (czytaj: 'n silnia’) jest iloczynem liczb od 1 do n
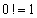
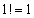
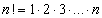
Dla wielkich liczb możemy obliczyć wartość n! z wzoru przybliżonego:
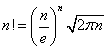
gdzie
e – jest podstawą logarytmu naturalnego
Już przy n = 20 wzór wykazuje mniej niż 0.5% błędu.
Algorytmy
Prosta metoda dla niewielkich liczb
Metoda została dodana do klasy Factorial.
public static long factorial(int n) {
if(n == 0){
return 1;
}
long sum = 1;
for(int i = 1; i < n + 1; i++){
sum = Math.multiplyExact(sum, i);
}
return sum;
}
Metoda wyrzuca wyjątek jeśli zostanie przekroczony zakres typu long.
Prosta metoda dla średnich liczb
Metoda została dodana do klasy Factorial.
public static BigInteger factorial(long n) {
if(n == 0){
return BigInteger.ONE;
}
BigInteger sum = new BigInteger("1");
for(long i = 1; i < n + 1; i++){
sum = sum.multiply(BigInteger.valueOf(i));
}
return sum;
}
Klasa Factorial
Wykonuje obliczenia dla dowolnych liczb. Ograniczeniem są możliwości komputera.
package callableimpl;
import java.math.*;
import java.util.concurrent.*;
/**
* Klasa do obliczeń n! w wątku
*
*/
public class Factorial implements Callable<BigInteger>{
private final BigInteger n;
public Factorial(BigInteger n){
this.n = n;
}
@Override
public BigInteger call() {
return factorial(this.n);
}
/**
* Oblicza silnię n! dla podanej liczby całkowitej
* @param n - liczba całkowita
* @return - zwraca n!
*/
public static BigInteger factorial(BigInteger n) {
if(rowny(n, BigInteger.ZERO)){
return BigInteger.ONE;
}
BigInteger sum = new BigInteger("1");
BigInteger i = new BigInteger("1");
while(mniejszy(i, n.add(BigInteger.ONE))){
sum = sum.multiply(i);
i = i.add(BigInteger.ONE);
}
return sum;
}
private static boolean rowny(BigInteger f, BigInteger s) {
return (f.compareTo(s) == 0);
}
private static boolean mniejszy(BigInteger f, BigInteger s) {
return (f.compareTo(s) < 0);
}
... Pominięto dwie wyżej listowane metody.
}
Użycie klas i metod
FactorialMain1
W klasie listujemy n! dla n = 1 do n = 100. Używamy metody Factorial.factorial(long n).
package callableimpl;
import java.time.*;
public class FactorialMain1 {
public static void main(String[] args) {
Instant startTime = Instant.now();
for (long i = 1; i < 101; i++) {
System.out.println(i + ": " + Factorial.factorial(i));
}
Instant endTime = Instant.now();
long time = Duration.between(startTime, endTime).toMillis();
System.out.println("Czas wykonania: " + time + (" ms"));
}
}
W wyniku na konsoli otrzymujemy:
1: 1 2: 2 3: 6 ... 100: 9332621544394415268169923885626670049 071596826438162146859296389521759999322991 560894146397615651828625369792082722375825 1185210916864000000000000000000000000 Czas wykonania: 40 ms
Klasa FactorialMain2
Chcemy obliczyć n! dla n = 200.
package callableimpl;
import java.math.*;
import java.time.*;
import java.util.concurrent.*;
public class FactorialMain2{
public static void main(String[] args) {
BigInteger n = new BigInteger("200");
ExecutorService es = Executors.newFixedThreadPool(1);
Future<BigInteger> f = null;
System.out.println("Start");
Instant startTime = Instant.now();
f = es.submit(new Factorial(n));
Instant endTime = Instant.now();
try{
System.out.println(f.get());
} catch (InterruptedException | ExecutionException e){
e.printStackTrace();
}
es.shutdown();
long time = Duration.between(startTime, endTime).toMillis();
System.out.println("Czas wykonania: " + time + (" ms"));
System.out.println("Koniec");
}
}
A oto nasz wynik:
Start 788657867364790503552363213932185062295135977 687173263294742533244359449963403342920304284 011984623904177212138919638830257642790242637 105061926624952829931113462857270763317237396 988943922445621451664240254033291864131227428 294853277524242407573903240321257405579568660 226031904170324062351700858796178922222789623 703897374720000000000000000000000000000000000 000000000000000 Czas wykonania: 0 ms Koniec
Zwróćmy uwagę, że czas wykonania jest mniejszy niż 1 ms. Powinniśmy czas mierzyć w nanosekundach.
Liczba ma 355 cyfr.

